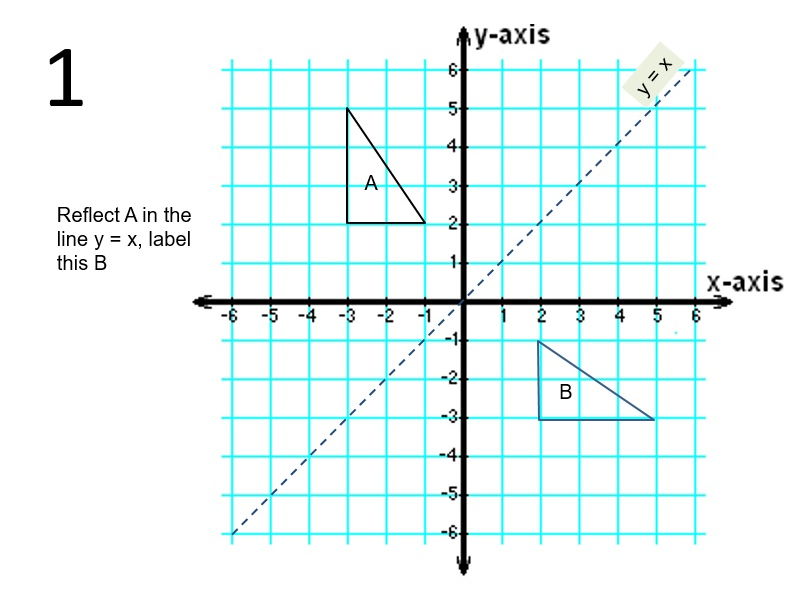
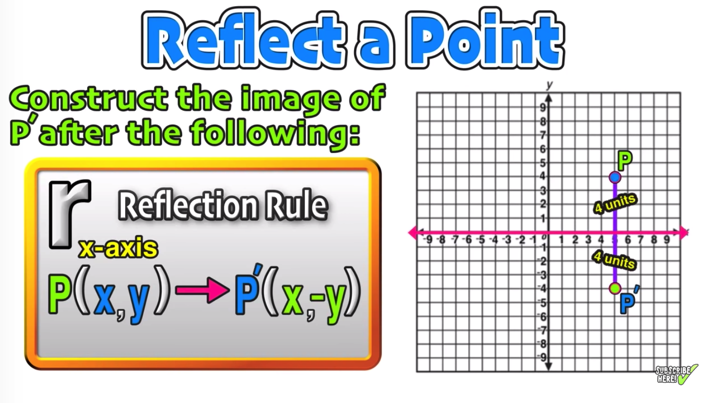
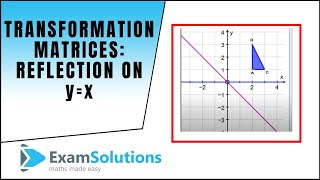
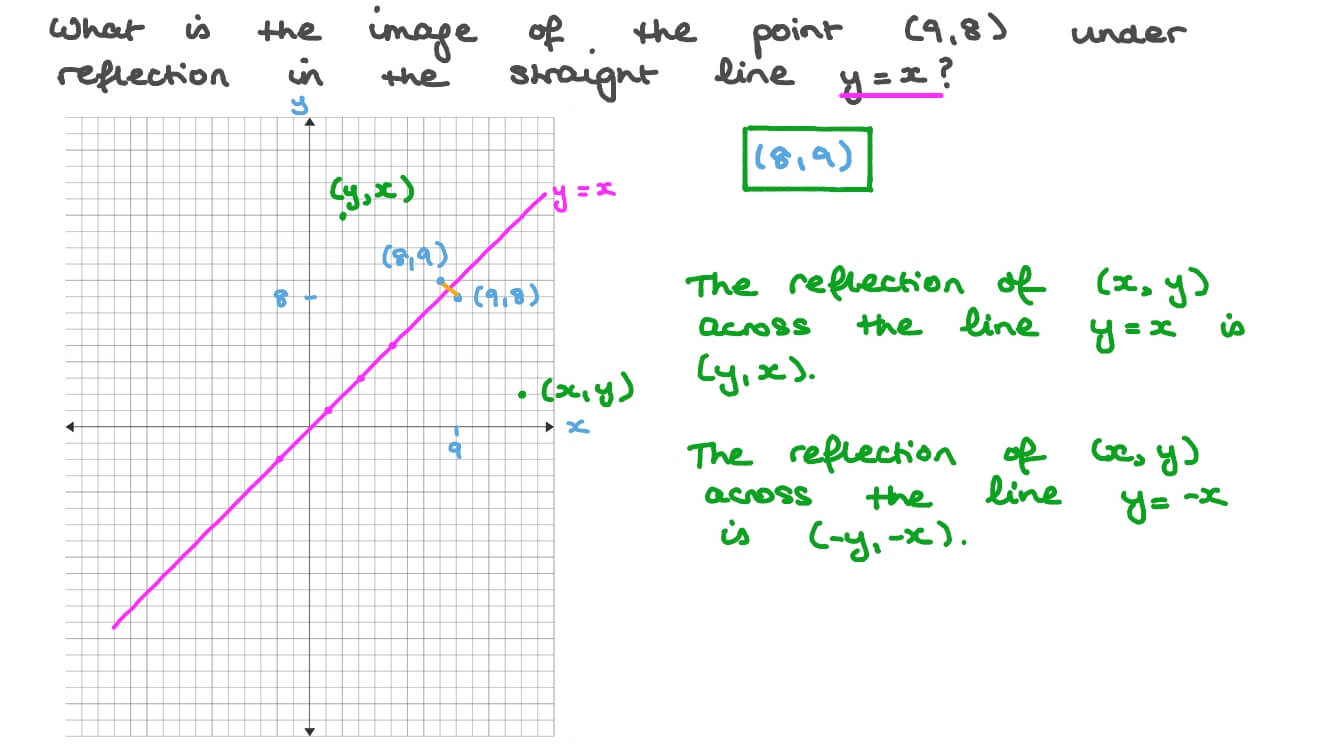
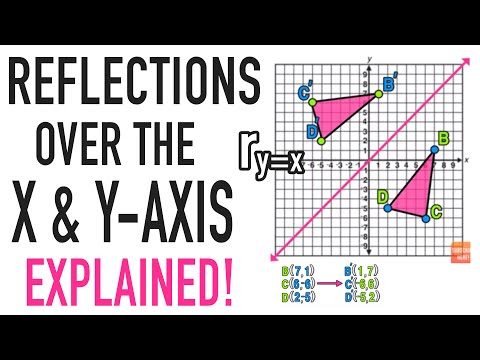
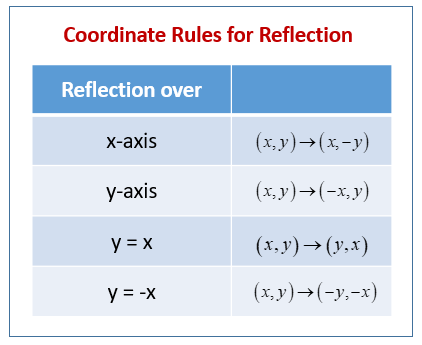
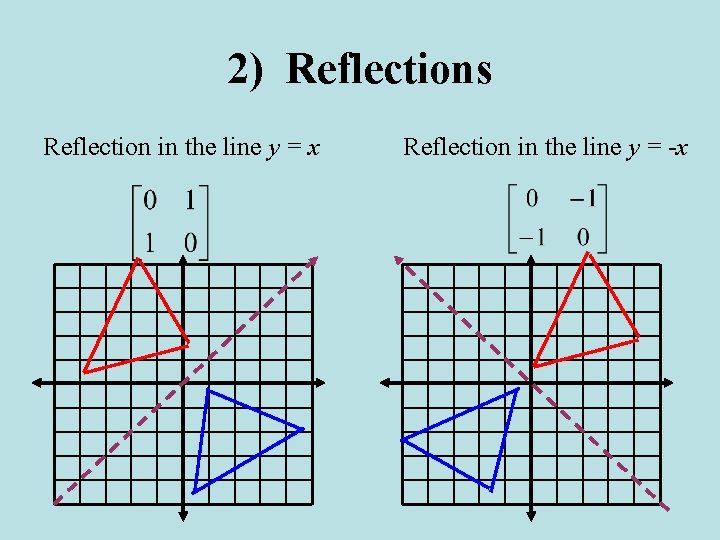
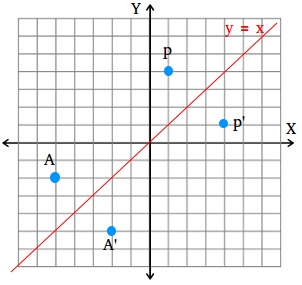
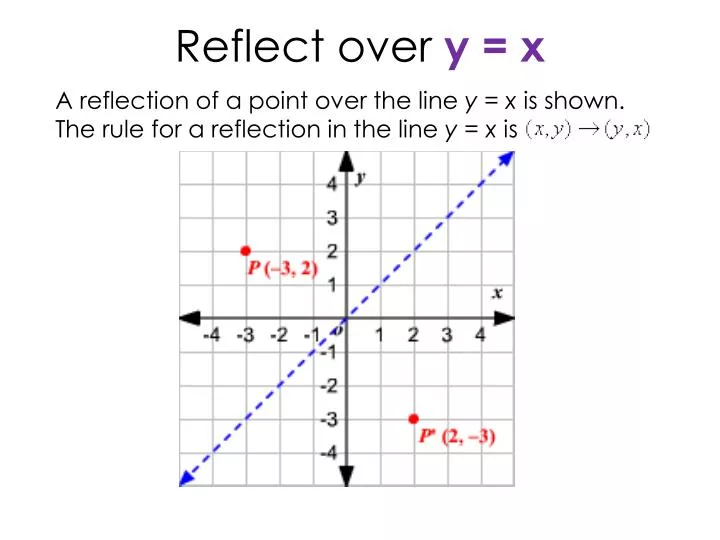
A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y AxisWhich transformation represents a reflection over the y = x line?A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $
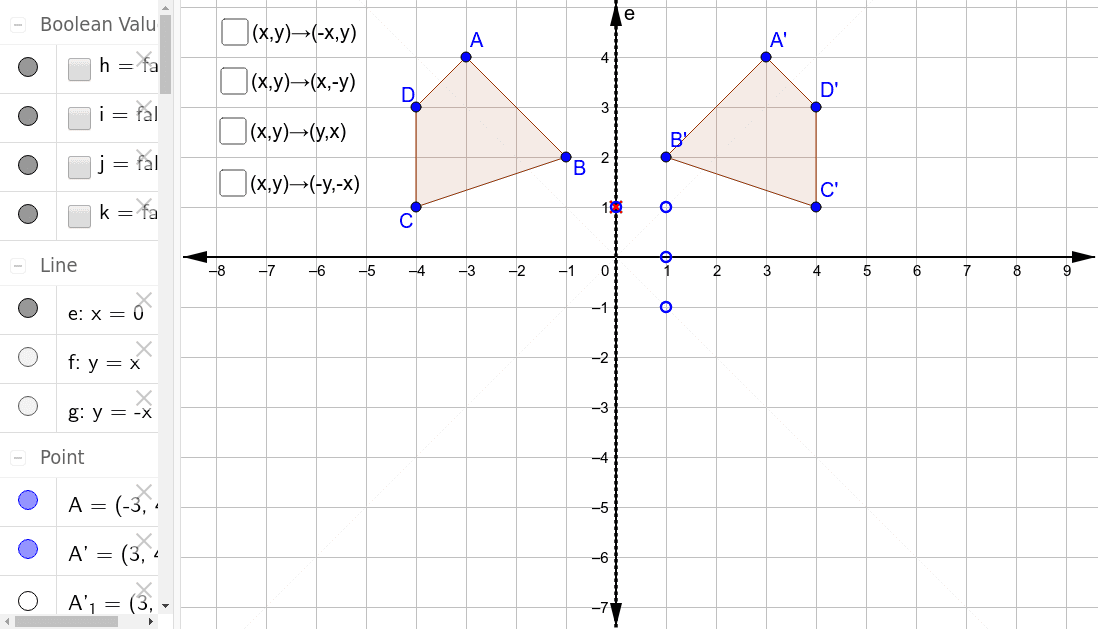
Reflections Through The Axes And The Lines Y X And Y X Geogebra
How to do a reflection across the line y=x
How to do a reflection across the line y=x-Reflecting shapes diagonal line of reflection Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organizationA graph was reflected in the line y = x Its Cheggcom 7 A graph was reflected in the line y = x Its reflection image is shown Determine an equation of the original graph in terms of x and y Y 5 А у су B 41 DW4 4 y = Question 7 A graph was reflected in the line y = x



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q
The coordinates of every point on the line y=x are the same after transforming (x,y) to (y,x) So, the inverse is the reflection of the graph of y=f(x) in y=x, which is symmetrical in itself and doesn't change Do inverse functions reflect over Y X?Answer (1 of 4) The line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I will select a point on line y=x illReflect over y = x Rotate 90°CC about (0,0) THEN reflect over the line y = 0 "Glide Reflection"
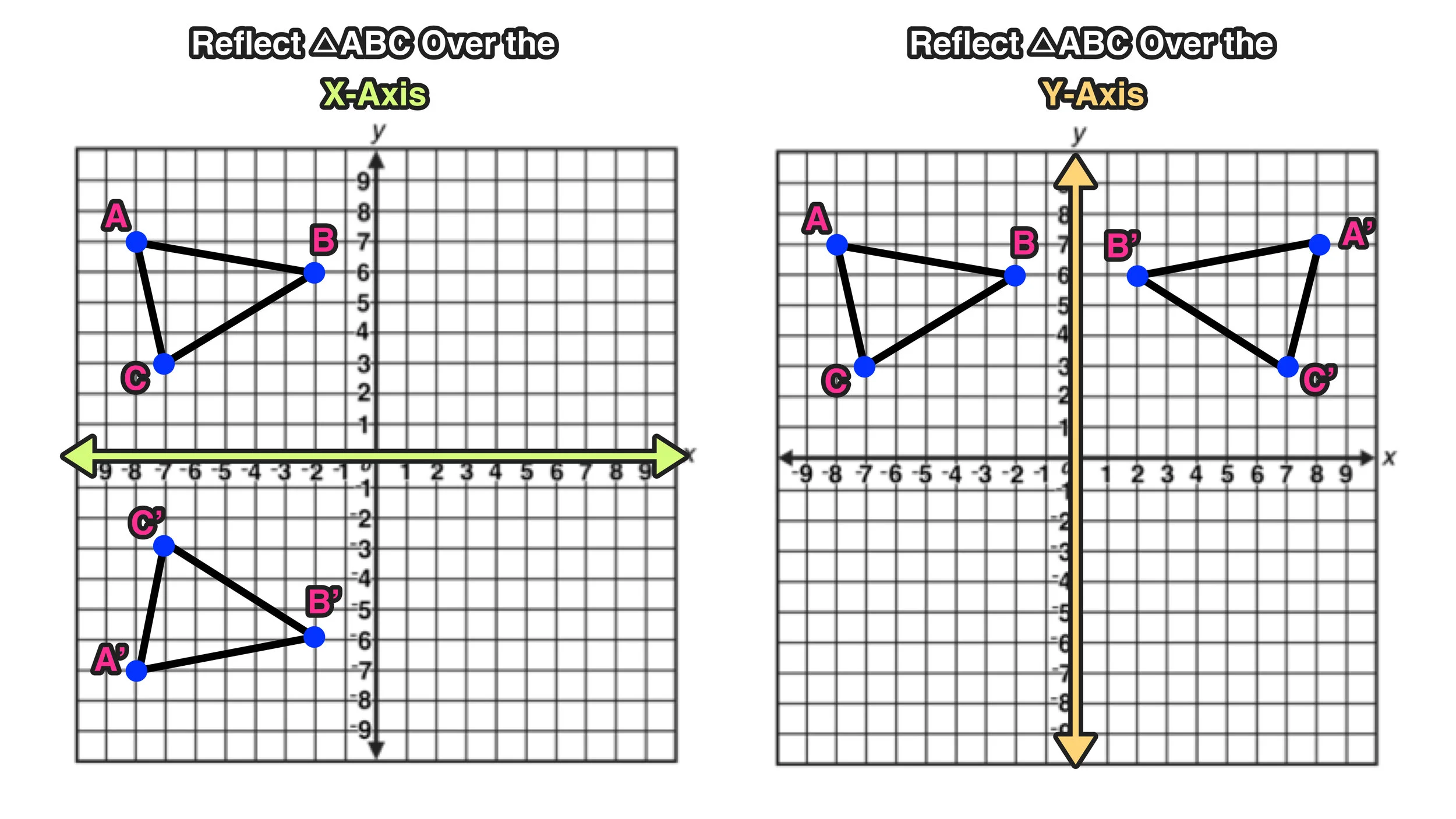
Learn about reflection in mathematics every point is the same distance from a central line Show Ads Hide Ads About Ads Reflection When the mirror line is the yaxis we change each (x,y) into (−x,y) Fold the Paper And when all else fails, just fold the sheet of paper along the mirror line and then hold it up to the light !Determining reflections (advanced) CCSSMath HSGCOA5 Transcript Sal is given two line segments on the coordinate plane, and determines the reflection that maps one of them into the other Google Classroom Facebook TwitterReflection in the line y = x y = x is an equation of the line which makes an angle of 135° with the positive direction of X axis ∴ Slope of the line y = x is m 1 = tan 135° = 1 Let P (x, y) be any point in the plane Draw perpendicular PM from the point P to the line y = x and produce it to the point P' such that PM = MP'
3 people liked this ShowMe Flag ShowMe Viewed after searching for reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1 You must be logged into ShowMe When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) the line y = x is the point (y, x) the line y =The resulting orientation of the two figures are opposite



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N
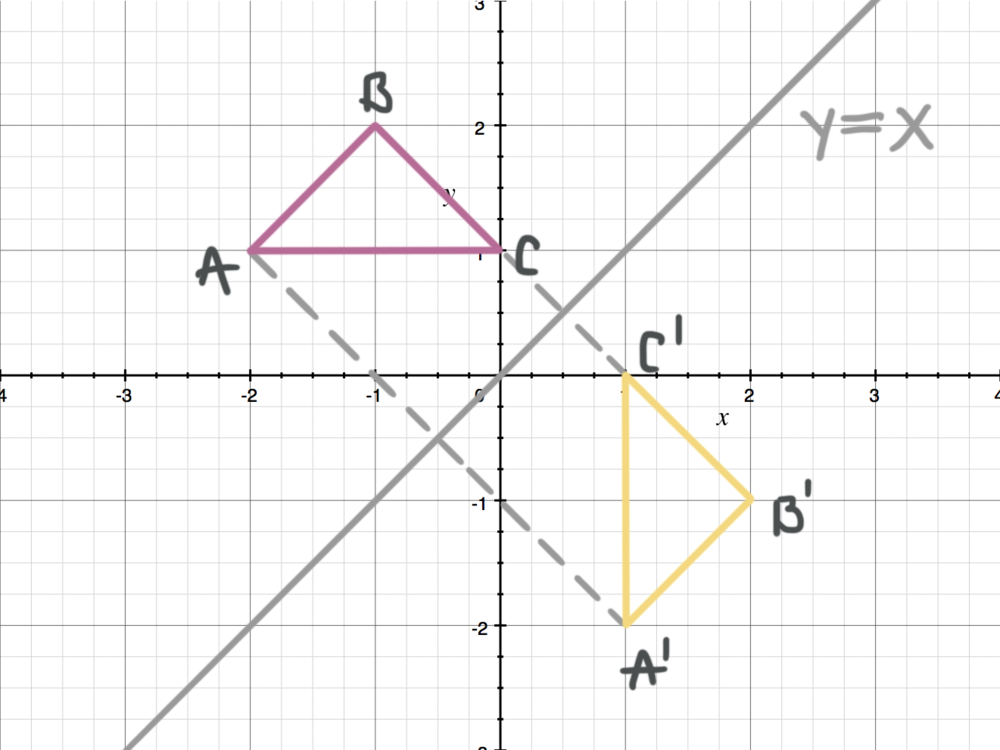



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
Reflect over y = x Rotate 90°CC about (0,0) Translate Dilated with scaled factor 2 centered at (0, 0) Get a ruler for today!Triangle ABC is translated using the rule (x, y) → (x 1, y − 4) to create triangle A′B′C′ If a line segment is drawn from point A to point A′ and from point B to point B′, which statement would best describe the line segments drawn?Answer (1 of 2) There are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joining PP′ is perpendicular to
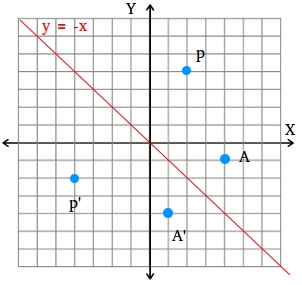



How To Find A Reflection Image



Math Alive Geometry 1
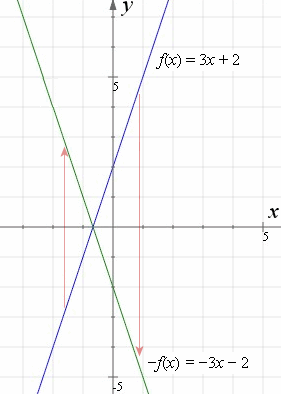
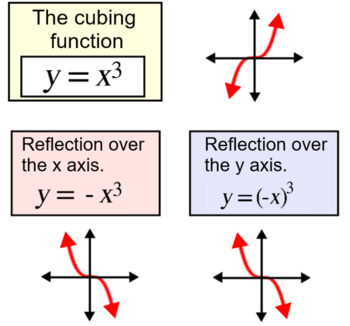
A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6)Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Y = f (x) y = f (−x) Remember, the only step we have to do before plotting the f (x) reflection is simply divide the xcoordinates of easytodetermine points on our graph above by (1) When we say "easytodetermine points" what this refers to is just points for which you know the x
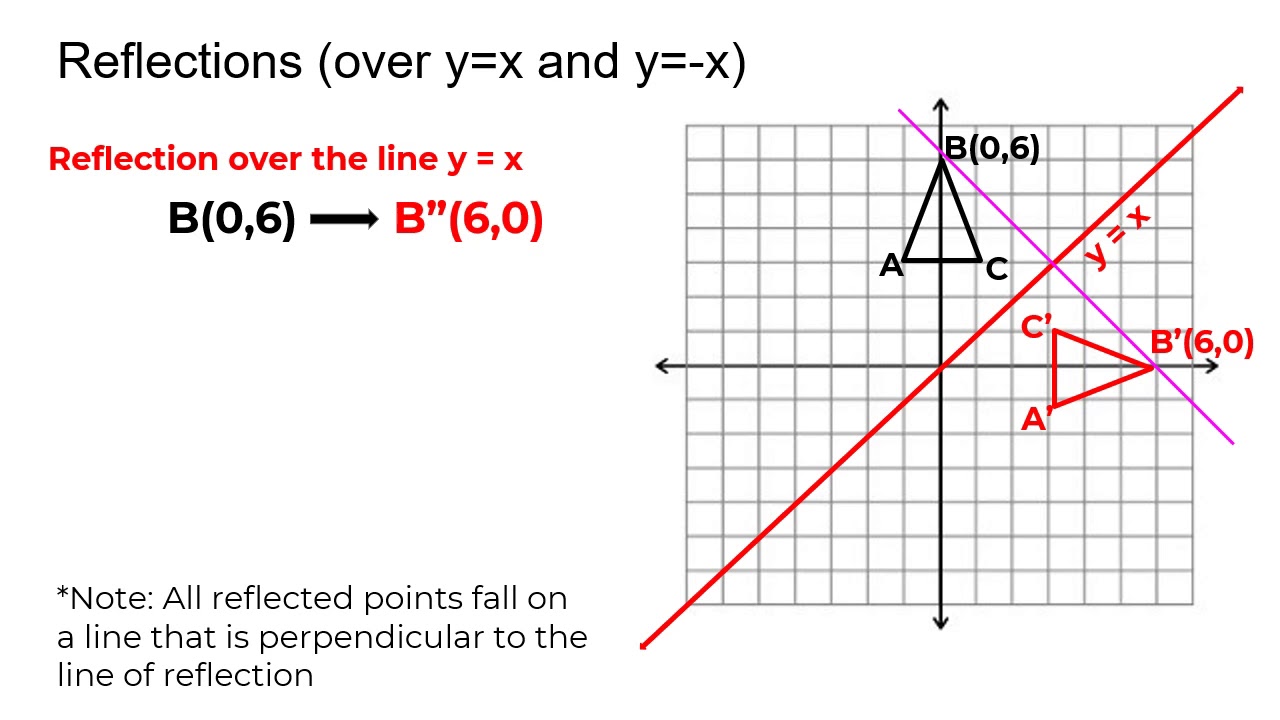



Reflection Over The Y X Line Youtube



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora
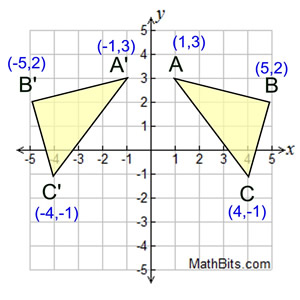
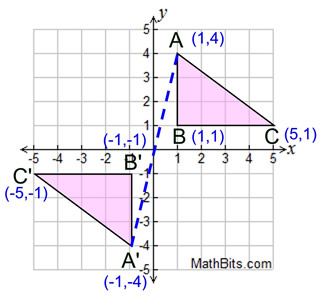
When you draw a line segment connecting the points A and A', the origin should be the midpoint of the line Therefore, The point of reflection in origin (0, 0), the image of the point (x, y) is (x, y) Hence, the coordinates of the triangle A'B'C are A' (1,4), B' (1,1), and C' (5,1)A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a line of symmetry using a reflection matrixReflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflection




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Diagonal Reflections In The Line Y X Teaching Resources
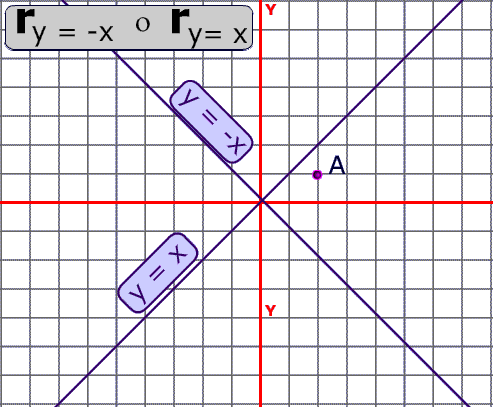
3 However, if we reflect y x= 2 about the line y = − 1, we do in fact get a function, namely y x= − −2 2 (see Figure 2) To see this informally, observe that y x= 2 reflected about the x axis yields the function y x= − 2For reflection about the line y = − 1, a line parallel to the x axis, note that (0,0) , the vertex of y x= 2, clearly maps to (0, 2)−MathematicsTransformation Geometry Line of Reflection y=x Slideshare uses cookies to improve functionality and performance, and to provide you with relevant advertising If you continue browsing the site, you agree to the use of cookies on this website"a translation of (x, y) → (x 1, y 5) after a reflection in the line y = x" You may also see the notation written as This process must be done from right to left Composition of transformations is not commutative As the graphs below show, if the transformation is read from left to right,



Reflections Math Analysis Functions



What Is The Image Of 2 5 Reflected Across X 2 Socratic
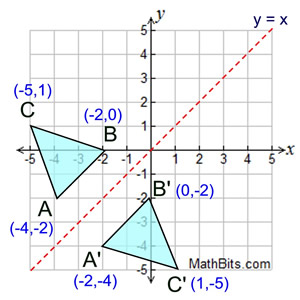
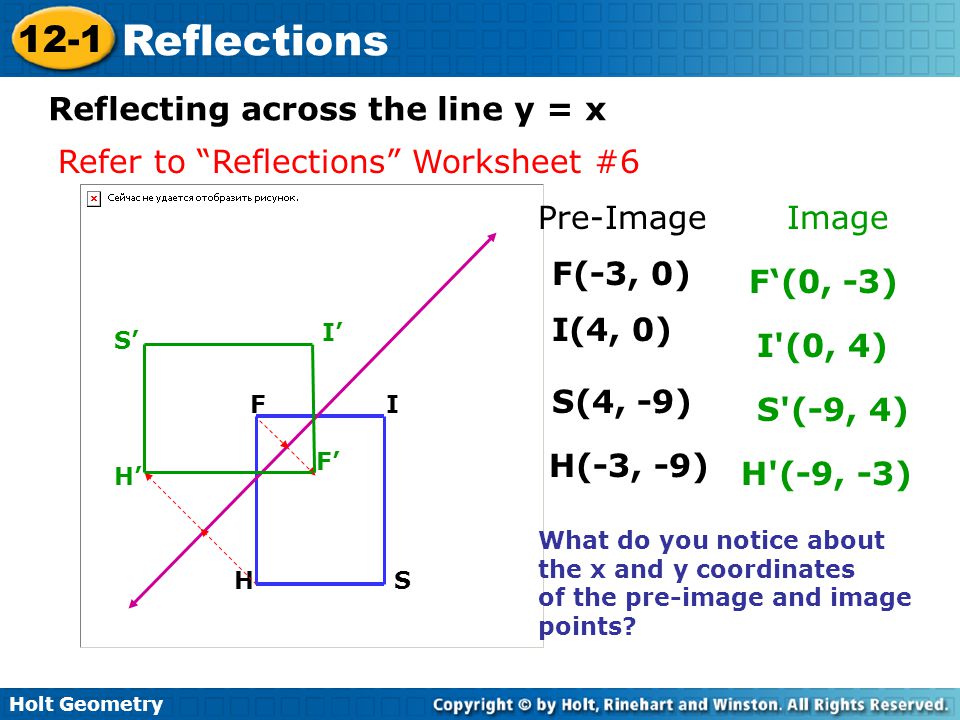
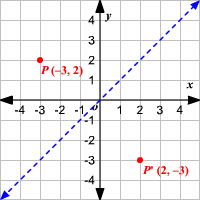
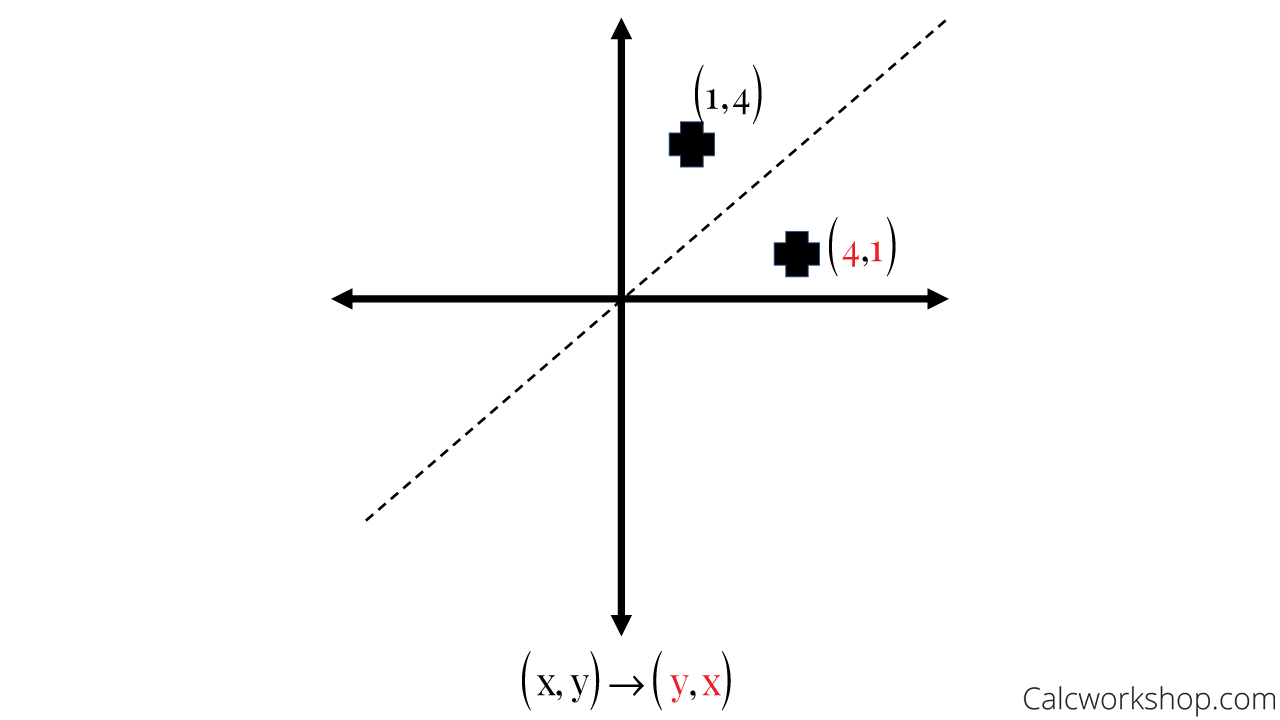
Remember this is a negative diagonal line through the origin Preview this quiz on Quizizz Quiz Reflections Over Line Y= X DRAFT 8th grade Played 0 times 0% average accuracy Mathematics 19 minutes ago by miss_saxtonThe reflection of the point (x,y) across the line y = x is the point (y, x) The reflection of the point (x,y) across the line y = x is the point (y, x) bullet Reflect over any linerefX4 Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure(x, y) → (y , x



1



Predicting The Reflection Of A Point When The Line Is Not Y X Maths Amino Amino
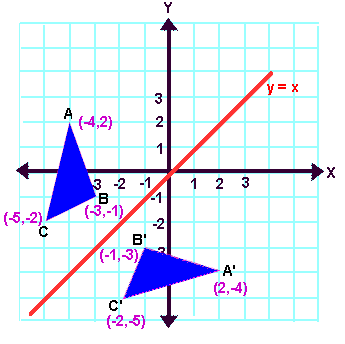
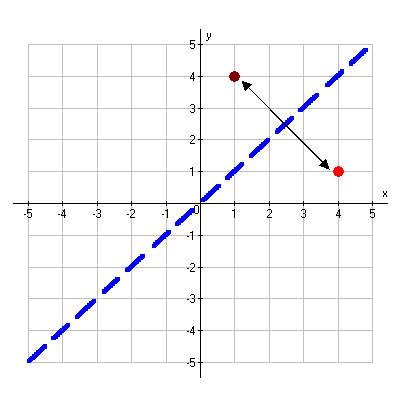
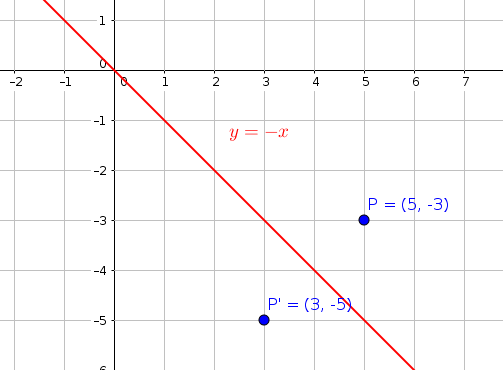
When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places and are negated (the signs are changed) The reflection of the point (x, y) across the line y = x is the point (y, x) P(x,y)→P'(y,x) or r y=x (x,y) = (y,x) The reflection of the point (x, y) across the line y = x is the point (y, x)If (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed; Find all zeros of f(x) = x^3 6x 7x 4 Enter the zeros separated by commas Enter exact value, not decimal approximations Write the equation of the line parallel to the line and passing through the point y=6, (3, 4)



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com



Reflection Transformation Matrix
Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxisA reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection y = −xApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflection



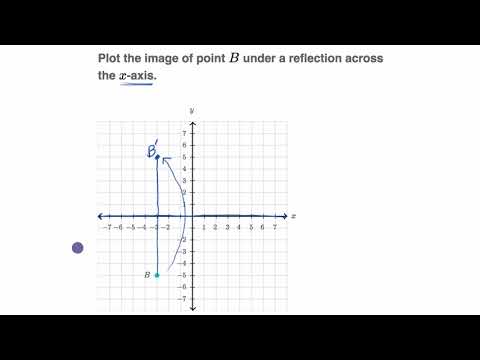
Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflection Mathbitsnotebook A1 Ccss Math
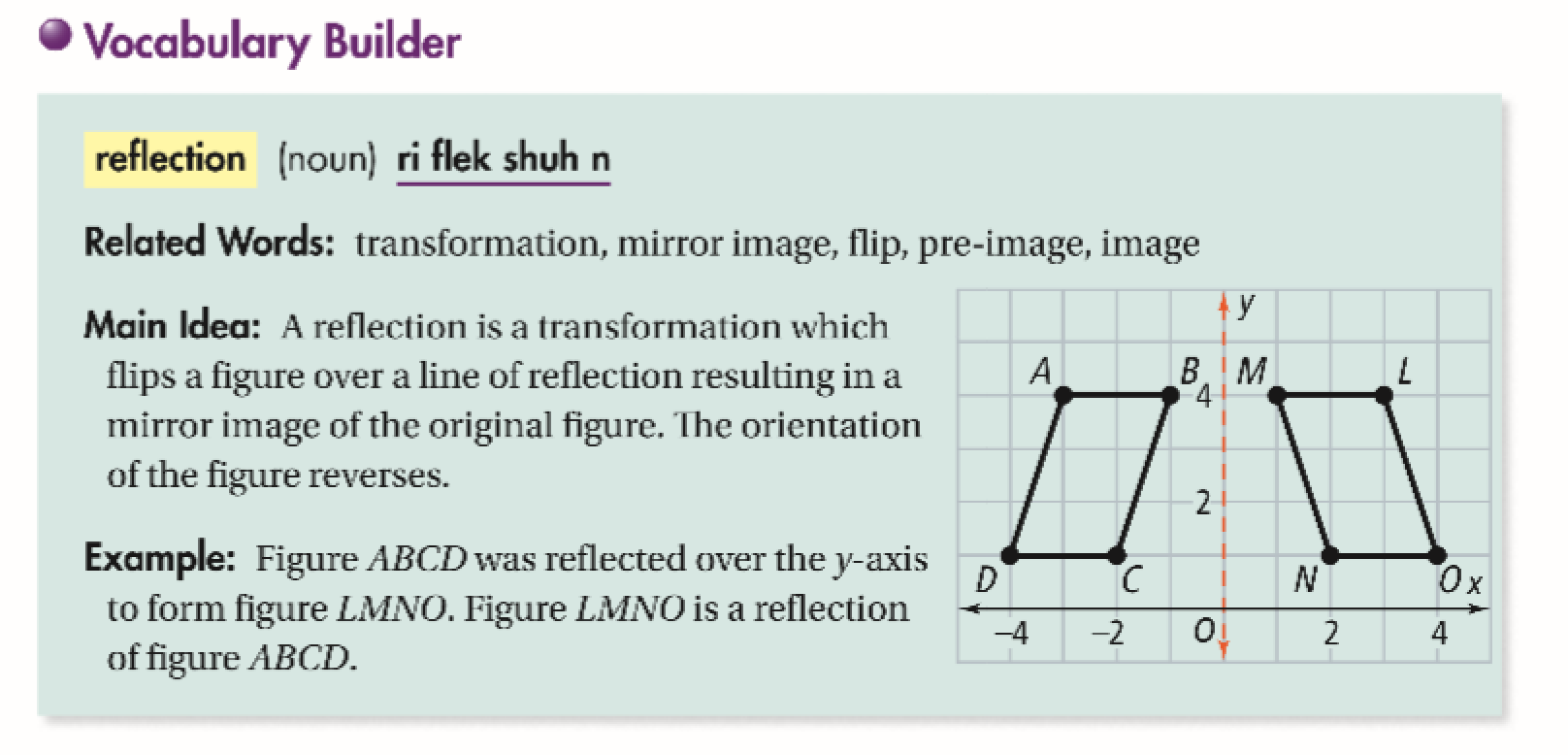
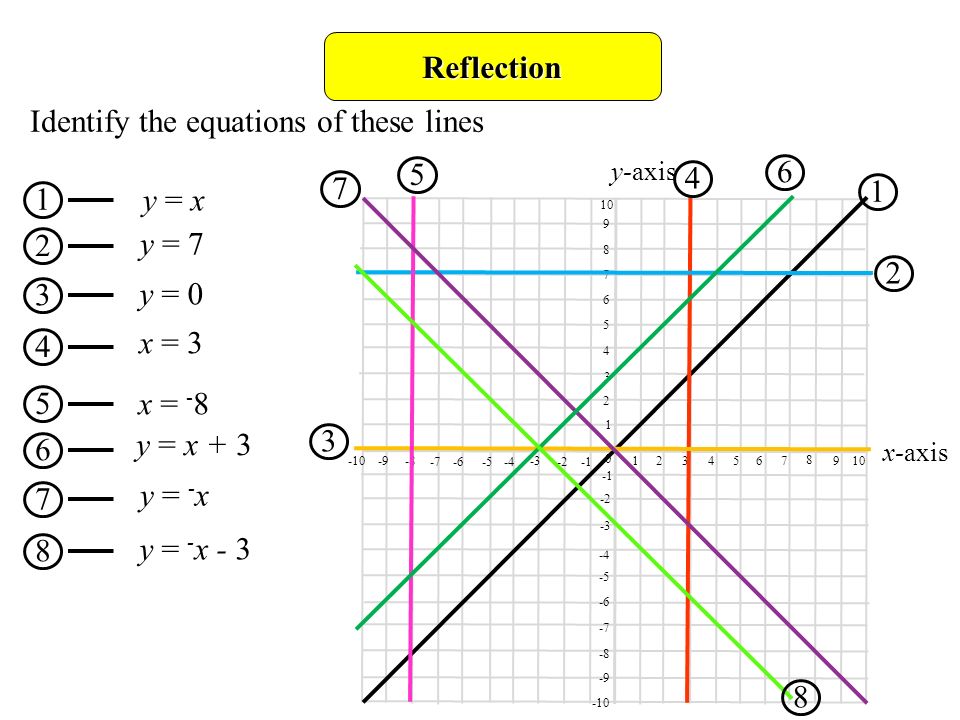
A reflection in a line produces a mirror image in which corresponding points on the original shape are always the same distance from the mirror line The reflected image has the same size as the original figure, but with a reverse orientationReflections and Rotations Summary Reflections and Rotations Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xA Formula to Reflect a Point in y = −x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinates The image below shows a general Cartesian coordinate being reflected in the line y = −x



Transformations Translations And Reflections



Reflection Mathbitsnotebook A1 Ccss Math
If you're asked to graph the inverse of a function, you can do so by remembering one fact aA point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxisFor a point reflection, we actually reflect over a specific point, usually that point is the origin $ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red a , \red b) $18 B 6 A point has the coordinates (0, k) Which reflection of the point will produce an image at the same coordinates, (0, k)?



Reflection Mathbitsnotebook A1 Ccss Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math
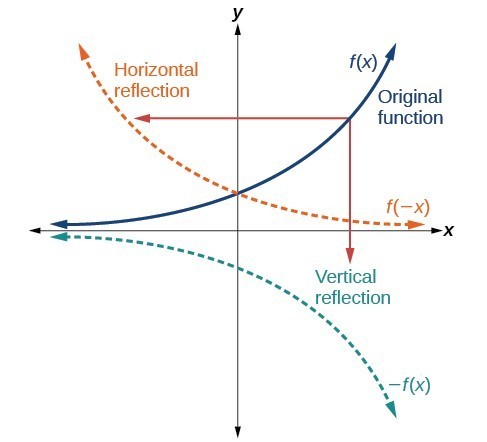
Key Points A vertical reflection is given by the equation y=−f (x) y = − f ( x ) and results in the curve being "reflected" across the xaxis A horizontal reflection is given by the equation y=f (−x) y = f ( − x ) and results in the curve being "reflected" across the yaxisThe rule for a reflection in the line y = x is ( x , y ) → ( y , x ) Reflection in the line y = − x A reflection of a point over the line y = − x is shownMatrices for Reflections 257 Lesson 46 This general property is called the Matrix Basis Theorem Matrix Basis Theorem Suppose A is a transformation represented by a 2 × 2 matrix If A (1, 0) → (x 1, y 1) and A (0, 1) → (x 2, y 2), then A has the matrix x 1 x 2 y 1 y 2 Proof Let the 2 × 2 transformation matrix for A be ab



Reflections Reflection In The Line Y X Revisely



1
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaPlay this game to review Mathematics What is the rule for a reflection across the y = x line?
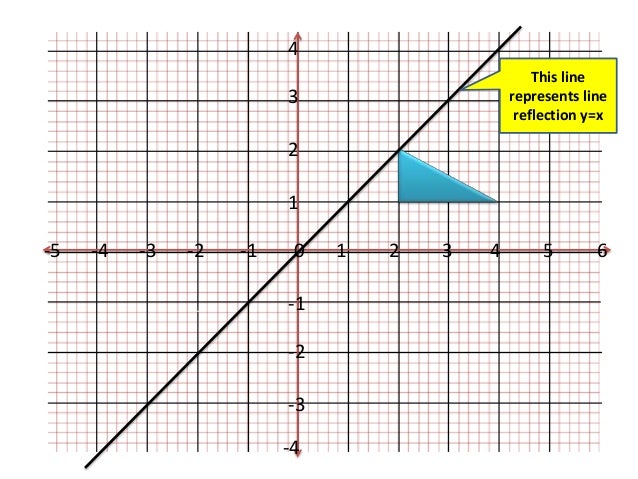



Lesson On Line Of Reflection Y X




Reflection Over Y X Math Geometry Showme
A reflection of the point across the xaxis a reflection of the point across the yaxis a reflection of the point across the line y =
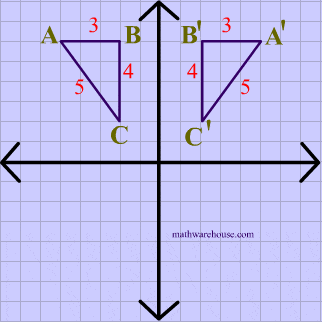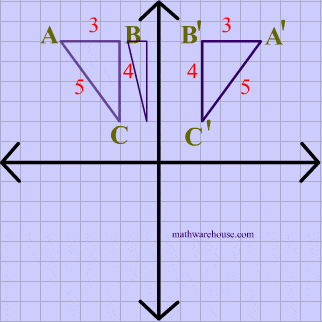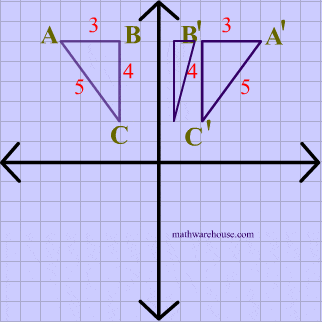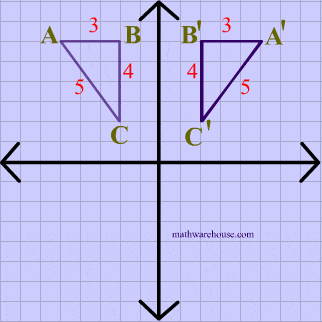



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
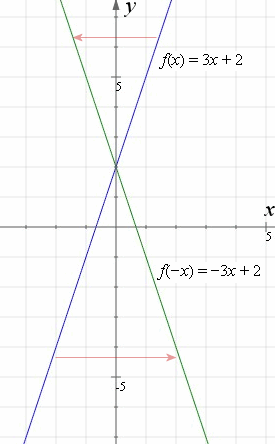



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
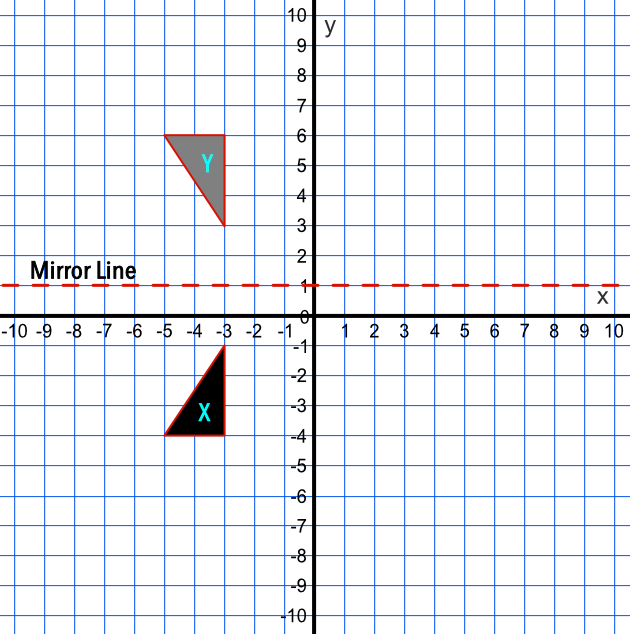



Reflection
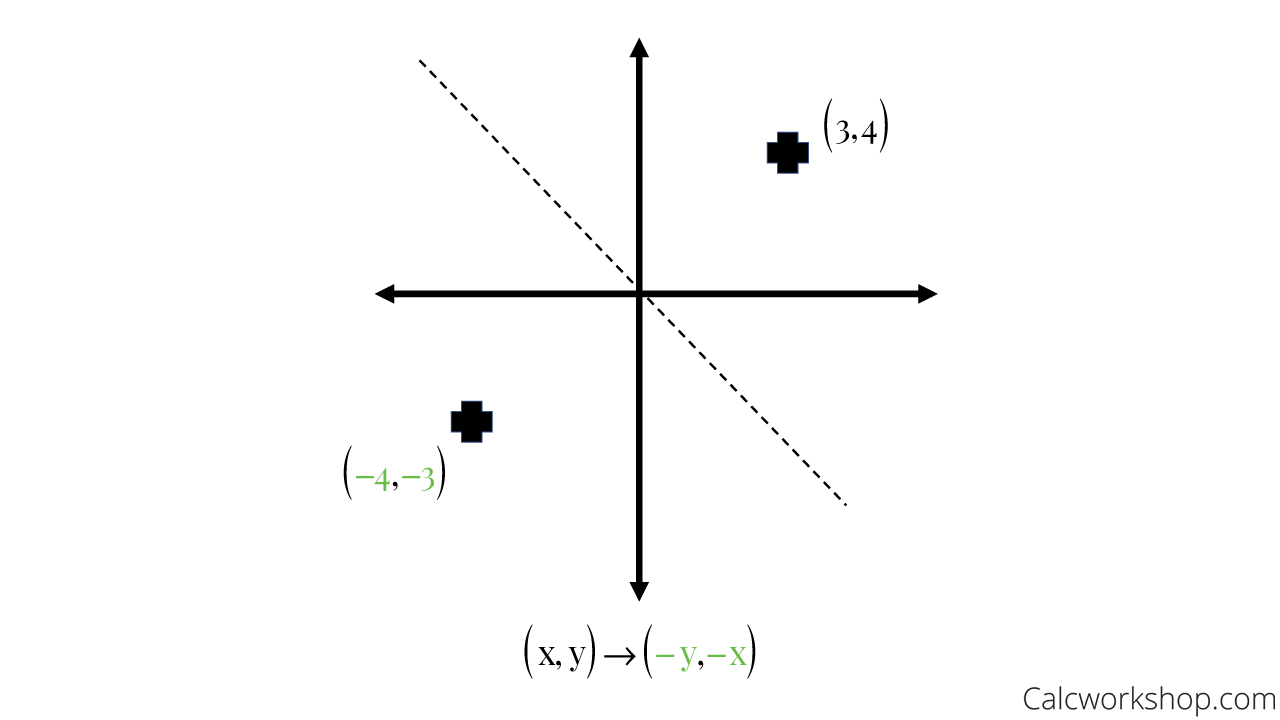



Reflection Rules How To W 25 Step By Step Examples




Common Reflections Key Stage 3




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics



Reflection Over Y X Activity Builder By Desmos



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative



Reflection Over A Line Expii
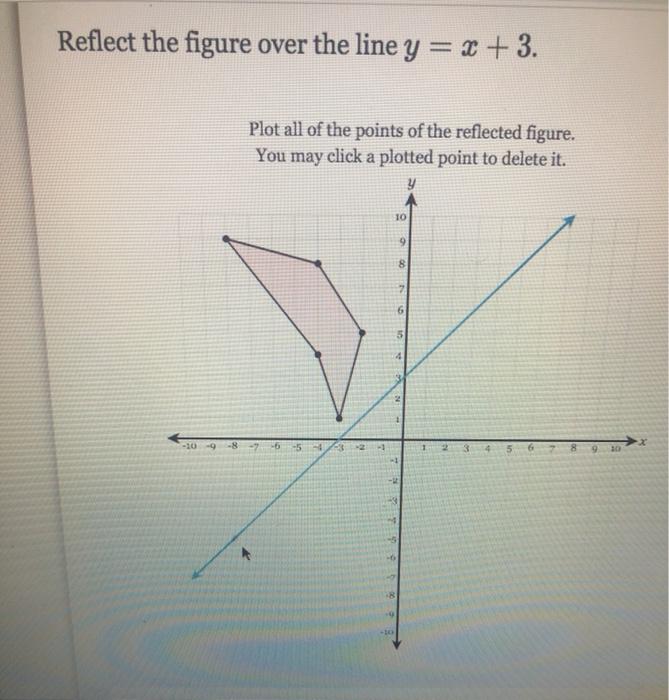



Solved Reflect The Figure Over The Line Y X 3 Plot All Chegg Com
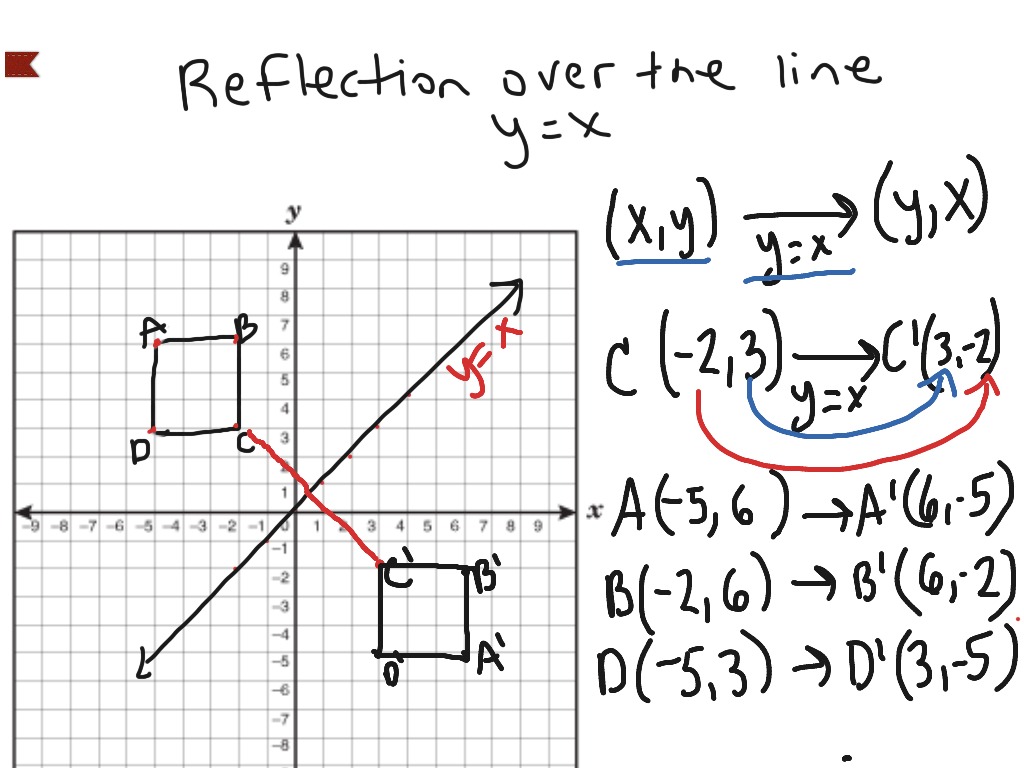



Reflection Over The Line Y X Math Showme




Reflections Ck 12 Foundation




Which Graph Shows A Reflection Across The Line Y X Brainly Com




10 Math Problems Transformation Reflection




Reflections Ck 12 Foundation




Transformation Rules Flashcard Flashcards Quizlet
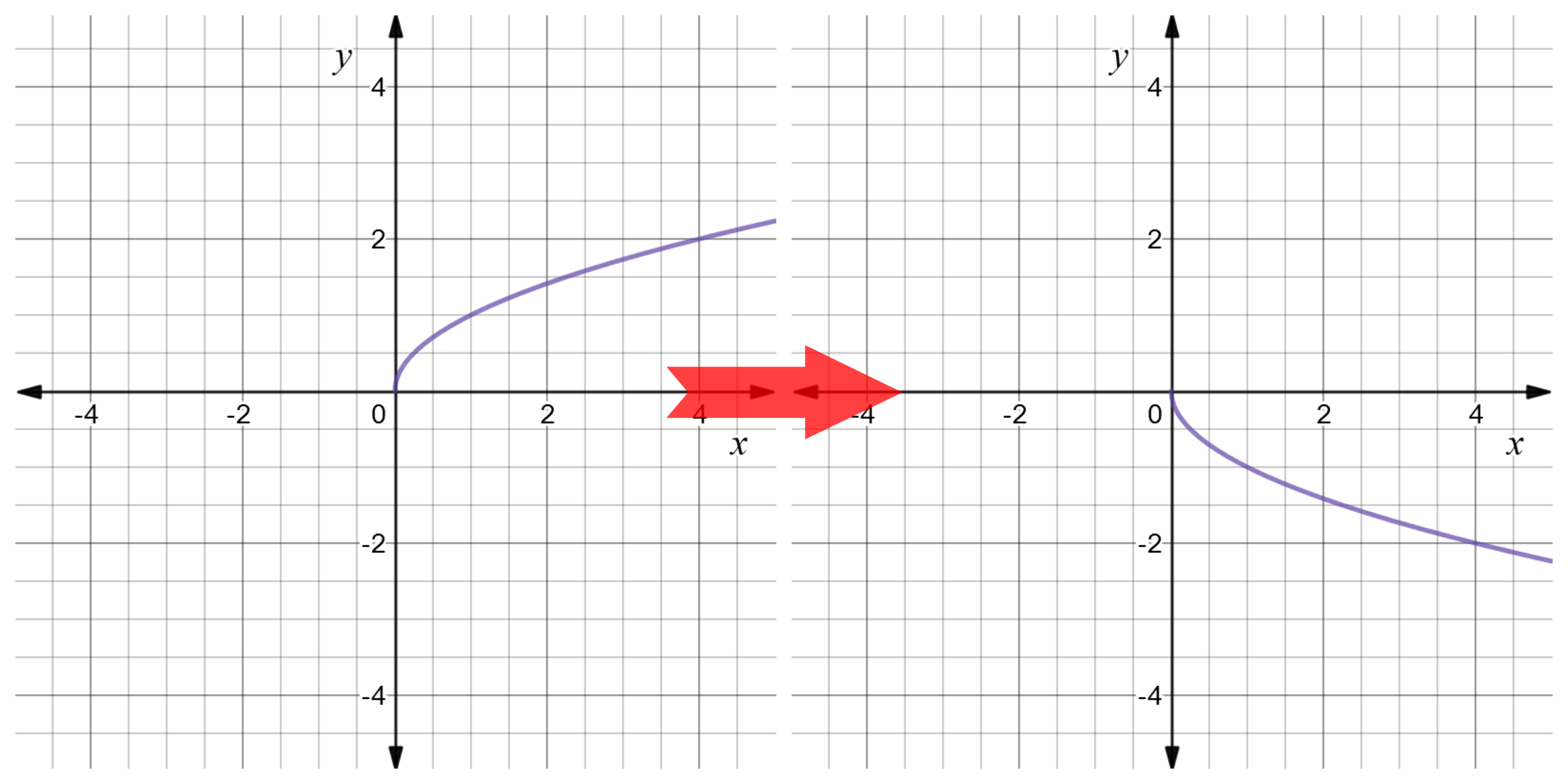



Reflect Function About Y Axis F X Expii




Translation With Geogebra Figure 2 Reflection Through Line Y X With Download Scientific Diagram




Reflection Of Point Using Graph Paper



Biomath Transformation Of Graphs



Reflection In Geometry Examples Solutions Videos Worksheets Games Activities




Algebraic Representations Of Reflections




D Reflection Across Y X Brainly Com




Picture Of Reflection Across Y Axis Reflection Math Math Reflection



4 4 Transformations With Matrices 2 Reflections And



Reflections Of Functions Over The X Y Axes Intro 2 Assignments For Smart



Math Alive Geometry 1



Geogebra Project Rotations And Reflections Math At Dis
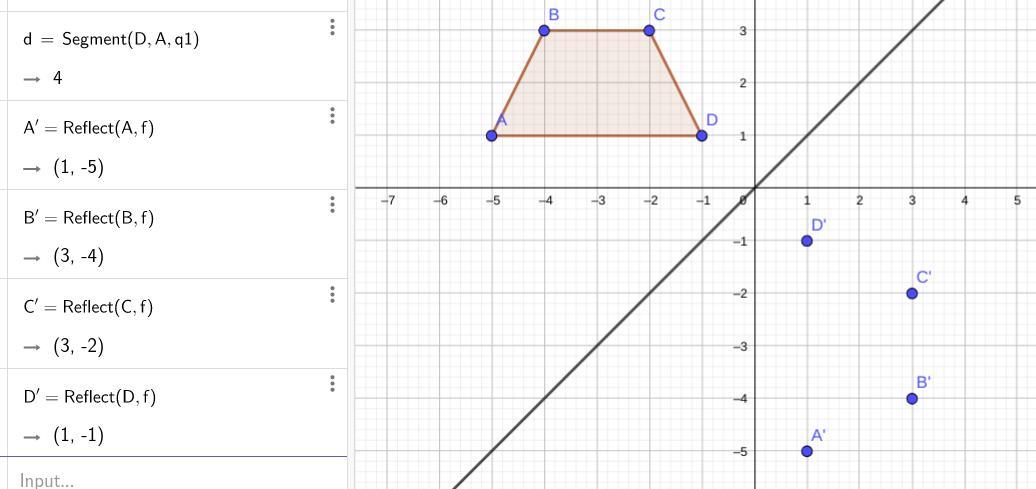



Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection And What Is The New Coo
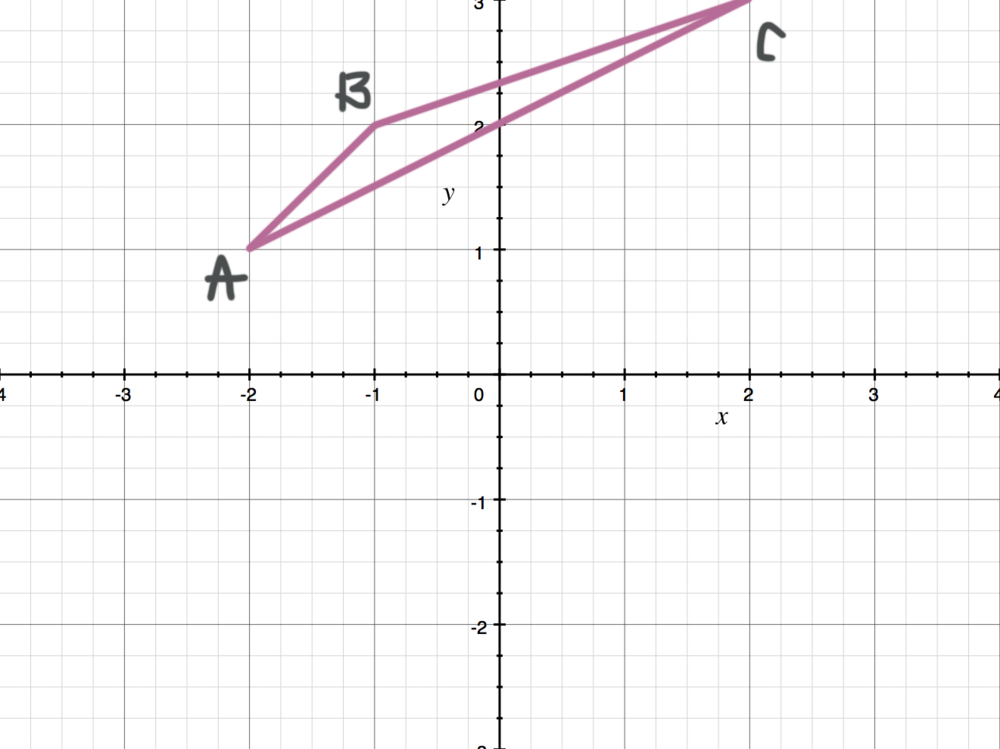



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
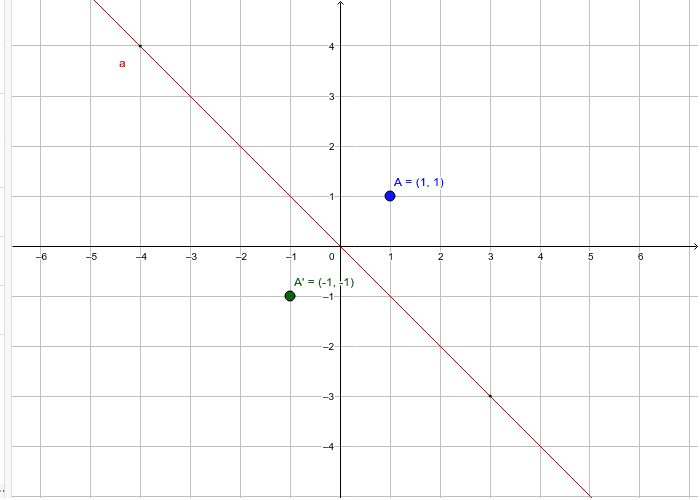



Reflections Across Y X Geogebra
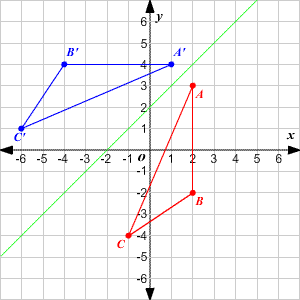



Transformations Of Graphs
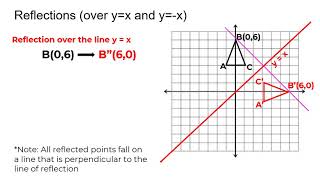



Reflection Over The Y X Line Youtube




Determine Equation For Reflection Of Equation Around Y X Line Mathematics Stack Exchange



Ixl Reflections




Reflection Objectives D Grade Reflect Shapes In Lines



Compositions Of Reflections In Mathematics Theorems Involving Parallel And Intersecting Lines Interactive



How To Find A Reflection Image



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra



Reflecting Points Video Reflections Khan Academy



Introduction And Review Information Ppt Download




Reflections Geometry Abroad




Picture Of Reflection In The Line Y X Reflection Math Common Myths Types Of Reflection
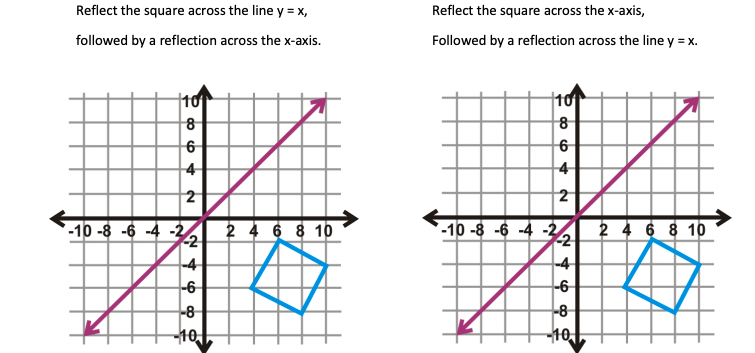



Solved Reflect The Square Across The Line Y X Followed By Chegg Com



Ixl Reflections



What Does It Mean To Reflect Over The Y X Line Quora




Rules For Reflections Read Geometry Ck 12 Foundation



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q



Reflections




The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange



Reflection Over The X And Y Axis The Complete Guide Mashup Math



1



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download



What Is The Reflection Image Of 5 3 In The Line Y X Socratic



Reflection Over The Line Y X Youtube




In The Xy Coordinate Plane Point P Is The Reflection Of The Point With Coordinates 3 1 Across The Line Y X Point T Is The Reflection Of Point P Across The Y Axis What



Reflection Rules How To W 25 Step By Step Examples



Translation Math



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id




Reflections Through The Axes And The Lines Y X And Y X Geogebra



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com
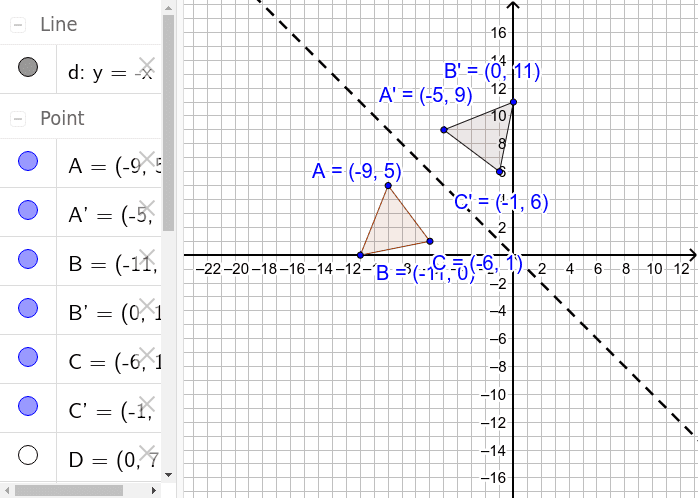



Reflection Over The Line Y X Geogebra
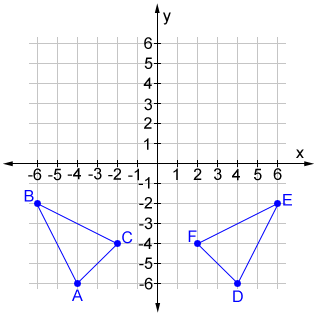



Reflection



Reflecting Shapes Video Reflections Khan Academy
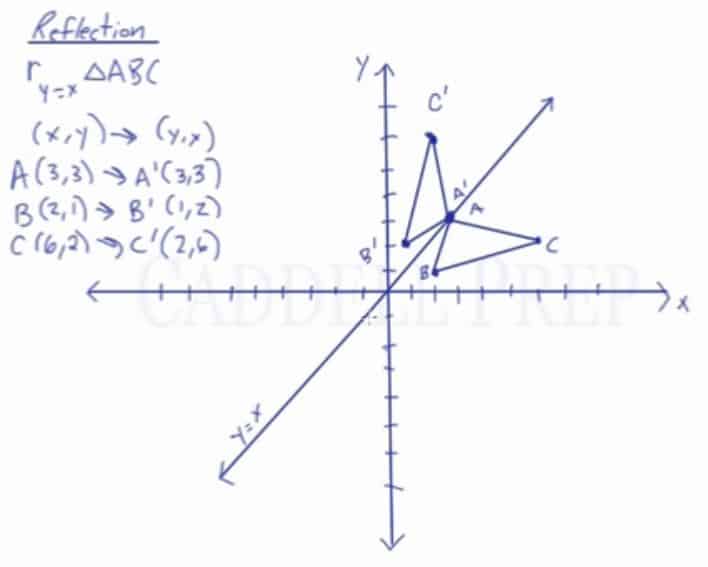



Learn About Reflection Over The Line Y X Caddell Prep Online
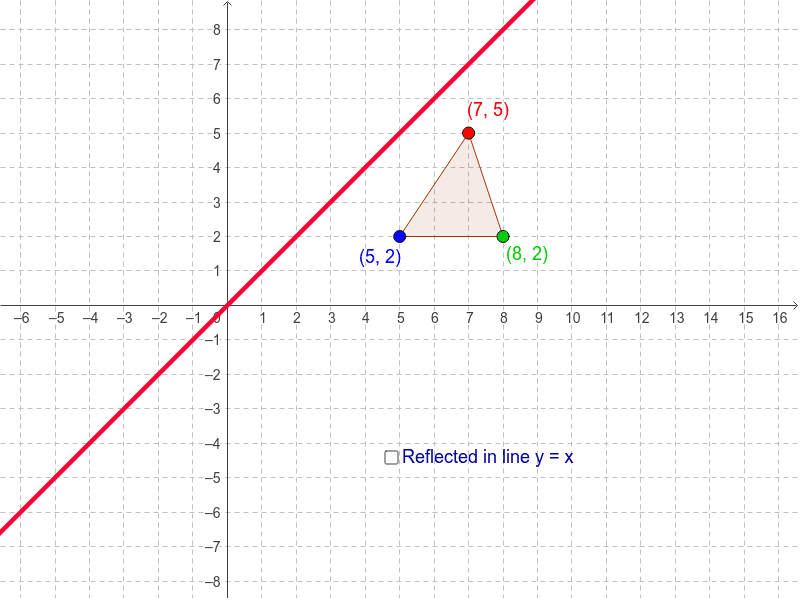



Reflection In The Line Y X Geogebra
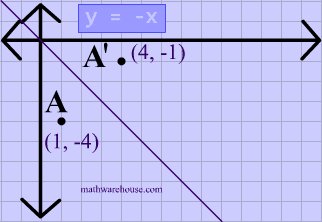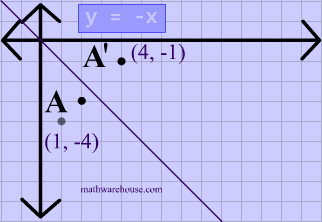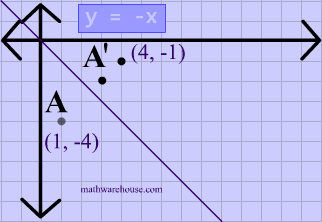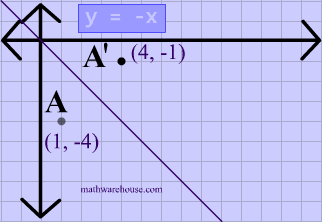



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero
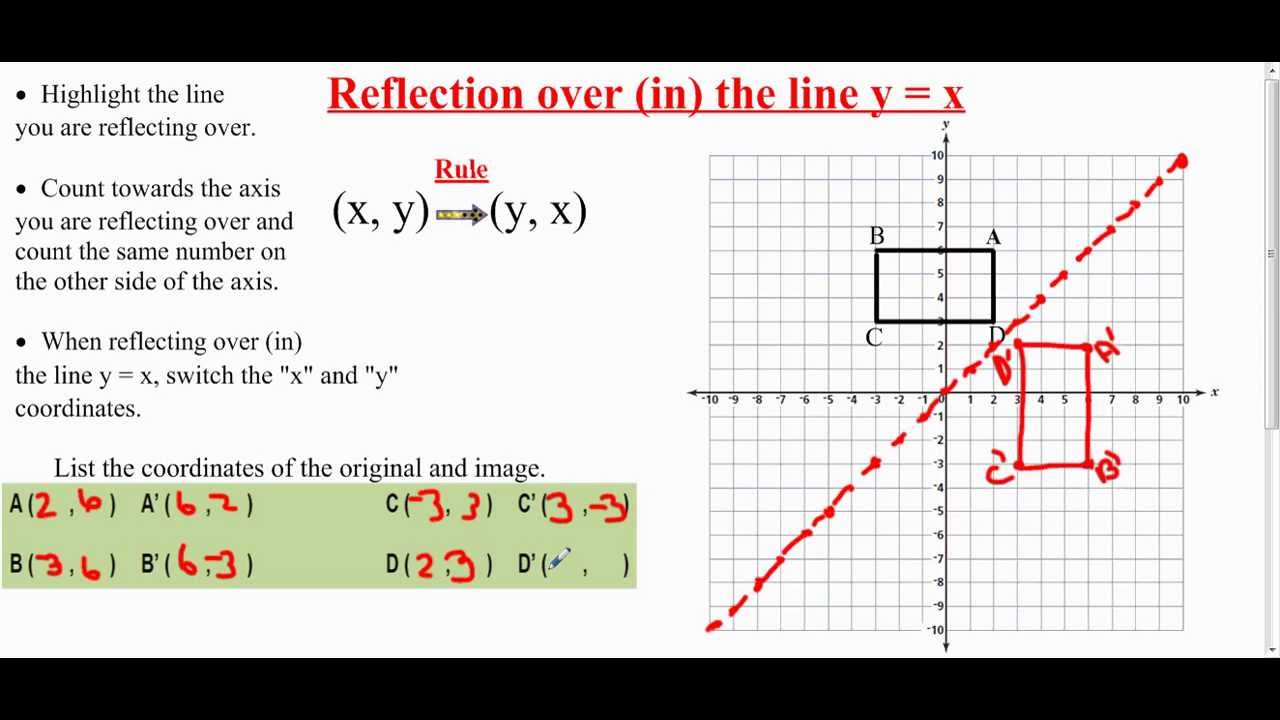



Transformation Reflection Over The Line Y X Youtube



2
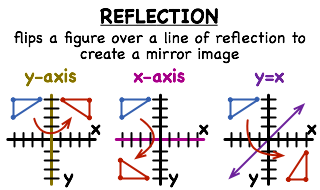



What Is A Reflection Printable Summary Virtual Nerd



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
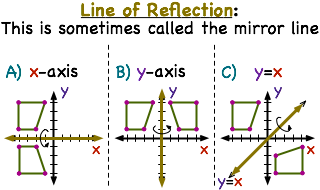



What Is A Line Of Reflection Printable Summary Virtual Nerd




How Are We Studying Transformations Differently By Eureka Math Eureka Math Medium




S1 Work For Problem Ii About Reflection Respect To The Y X Line But Download Scientific Diagram



Reflection Of A Point In A Line Msrblog




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



0 件のコメント:
コメントを投稿